Edit 2022-04-16: fix grammar

An edited version of this post has been published in two parts on heurekadevs.com: first part, second part.

How is the float and list data types represented in Python? Why do they take up so much memory? Why are some operations on them so slow? And why so many people turn to third party libraries, such as numpy?

In this article, we take a closer look at the implementation of two Python data types: float and list. We will see that with the flexibility of dynamically typed language, Python, come drawbacks in the form of added complexity and bigger memory requirements.

Throughout the post, I make a few simplifications (e.g. regarding any reusing of objects by the interpreter) to keep it brief. However, there should not be much loss of generality when we think of arbitrarily large lists and random floats.

Also, I describe these structures as they are implemented in CPython (specifically CPython 3.10.0).

PyObject

Let me start by saying that all data types in Python are objects. There are no primitive types.

On a lower level, every object “inherits” from PyObject struct. More precisely, because the CPython is in C, inheritance is implemented by holding an instance of the predecessor class. This provides an option to cast a pointer to every object to a pointer to PyObject (in C++, a pointer to a descendant can be cast to a pointer to a predecessor). This casting possibility is an important feature, as we will see later.

The PyObject struct contains a reference counter and pointer to a type:

typedef struct _object {
    _PyObject_HEAD_EXTRA
    Py_ssize_t ob_refcnt;
    PyTypeObject *ob_type;
} PyObject;

where _PyObject_HEAD_EXTRA is a macro for creating two pointers forming a doubly-linked list of objects for the garbage collector (to be able to handle self references):

typedef struct {
    // Pointer to next object in the list.
    // 0 means the object is not tracked
    uintptr_t _gc_next;

    // Pointer to previous object in the list.
    // Lowest two bits are used for flags documented later.
    uintptr_t _gc_prev;
} PyGC_Head;

These pointers are created for, among others, list, some tuples, some dicts or user defined classes, but not for types that can not hold references to themselves (e.g., int, float, …) because those can be collected using a simple reference counter. There is brilliant documentation of Python’s garbage collector.

pyobject

PyFloatObject

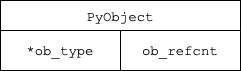
The float object contains an instance of PyObject and the value itself, which is actually C double (64-bit floating point number) which may be slightly confusing for a developer used to C-family language.

As a result, a float object uses 24 bytes of memory on a 64-bit system (8B for pointer on the object type, 8B for the reference counter and 8B for its value).

The implementation of PyFloatObject:

typedef struct {
    PyObject_HEAD
    double ob_fval;
} PyFloatObject

where PyObject_HEAD is just a macro for creating a PyObject.

Let us check the size of a float:

import sys
a = 1.0

print(sys.getsizeof(a))
# result: 24

float

Intermission about Cache

The main memory in a computer is much slower for common operations than what would be optimal for a CPU. To speed up computation, modern computers use a faster, and smaller memory called cache (or more commonly several differently fast and sized caches). Reading from a cache is about 10-100 times faster than reading from the main memory.

When an address in memory is accessed, the CPU loads a whole block of bytes into the cache (much more than needed, usually). If the required block is already present in the cache, the main memory does not need to be accessed and the computation is faster. If, however, it is not present (so called cache miss), the CPU needs to load it, which is slow. We want to reduce the number of misses as much as possible.

There are two classes of algorithms which take caches into account: cache-aware and cache-oblivious. Cache-aware algorithms assume or know the parameters of the cache, such as the number of caches, size of the block, number of blocks that fit into a cache,… This is often infeasible - most programs run on various hardware. Cache-oblivious algorithms do not know nor assume (almost) anything about caches, they just perform faster when a cache is present.

An example of a simple cache-oblivious algorithm is a sequential scan of an array (general C-like array, not the Python array module): when an element is accessed, a sequence of bytes surrounding the element is cached. When the next element is accessed it is most likely already present in the cache (assuming some common block eviction strategy, like “last-used-evicted-first”). The number of cache misses is minimal (optimal) for a sequential array scan.

On the other hand, scanning a linked list is inefficient with respect to caches. With reading one element, and loading a block of surrounding bytes into the cache, no other element in the list is likely to be present already present in the cache (assuming the list is arbitrarily long, and cache size is constant). Hence, reading almost every item makes a cache miss.

If the cache is about n times faster than the main memory, such scan is about n times faster in an array than it is in a linked list (this is simplified and other factors influence the performance).

For a deeper understanding of cache-oblivious algorithms, see the “Cache” chapter in Data Stuctures lecture notes by Mareš or Demaine 2002.

Back to Python…

PyListObject

As list in Python is able to hold objects of different types, and there is no need to specify the types in advance (like it is in a statically typed language, like C/C++/…), you are probably guessing there has be some overhead for this convenience.

And overhead there is. In both memory requirements and the time complexity of some common list operations (we will see later).

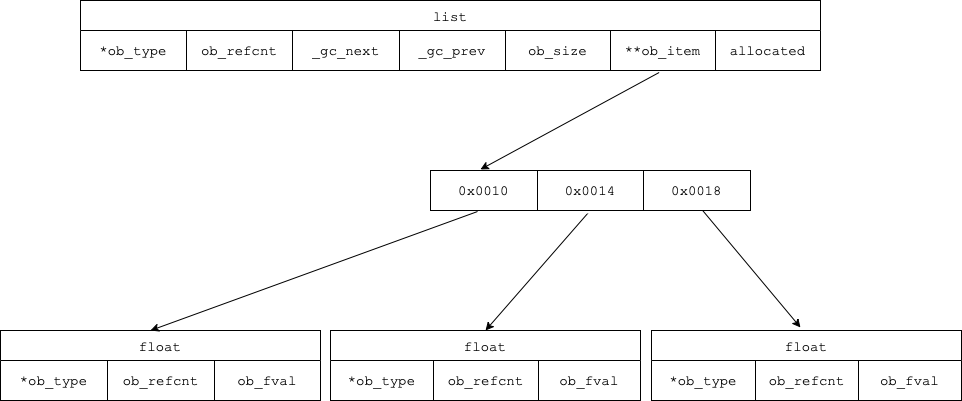
In order to fit objects of various, previously unknown types, list does not store the objects directly but only keeps a pointer to an array of pointers (of type PyObject) to the objects it holds. Keeping the pointer to an array, instead of just storing the array directly in its memory space, allows the list to have a variable length. And as we previously established, pointers to all Python types can be cast to a pointer to PyObject, meaning any set of objects can be stored in a list.

On top of the array of pointers, it holds PyVarObject (a base class for variable length containers in Python) which apart from a PyObject, it also contains a counter for the number of elements stored in it. Because it is a variable length array, it over allocates (to be explained later), so it holds a variable for the number of bytes allocated. And because list can “contain” (hold a reference) to itself, it has to have those two pointers for garbage collection.

The structure then looks like this:

typedef struct {
    PyObject_VAR_HEAD
    PyObject **ob_item;
    Py_ssize_t allocated;
} PyListObject;

where PyObject_VAR_HEAD is a macro for creating a PyVarObject.

Let us check the size of a float:

import sys
a = []

print(sys.getsizeof(a))
# result: 56

Beware that this is architecture specific, version specific, and most-likely OS specific and the size (or its calculation) might slightly differ. I have tested it on a x86 macOS.

The size of an empty list is not an issue if there are a lot of elements in it. But if, for example, we want to imitate a multidimensional array using list of lists of … list, then the overhead size of a list can become significant.

list-float

Operations on List

Firstly a list needs to be created. If the number of elements to be stored in it is not known in advance, one usually creates an empty list and then appends the objects to it.

However, if the number of items is known, then it would be faster (and more memory efficient) to create a list with the exact required size. This brings us to the append method.

append

Readers familiar with “flexible” arrays, should feel free skip the next few paragraphs.

Let us imagine we want to have an array/list but we do not know the number of items that will be added to it at runtime. If the allocated space of the array/list would accommodate exactly the number of items currently in it, it would have to be reallocated with every added item (resulting in O(n) complexity per append, where n is the current number of items).

To overcome the reallocation preceding every append, we always allocate little more space than necessary. If the allocated space is large enough (a multiple of the number of items), the amortized time complexity of append can be brought down to O(1). Amortized, in this context, basically denotes the average time complexity of an append in a series of appends. The worst-case complexity can be worse than the amortized complexity (it happens, when the reallocation is performed)

Similar claims hold also for remove operation and array/list shrinking. Note: when the array only grows, amortized complexity is the same as average complexity, but once removal of elements and “shrinking” of the array is allowed, there is a difference, but I won’t go into that.

See Mareš’s book for a description of amortized analysis.

What is interesting in CPython, is how the list is actually grown.

Python increases the space for the list by approximately a multiple of 1.125. The newly allocated memory after reallocation:

new_allocated = ((size_t)newsize + (newsize >> 3) + 6) & ~(size_t)3;

where new_size is the number of items in the list (after appending the last item). It basically says that the newly allocated memory is news_size * 9/8 + 6 but with the last two bits set to 0 (making the final number divisible by 4). Note: the factor is a little bit different for very small lists.

Why is the factor so small and computed in such a way? I would be happy to know. In C++, the growth factor of std::vector in GCC is 2, and in Microsoft compiler, it is reportedly 1.5. I suspect that since objects in Python are relatively large, the interpreter does not want to waste much space.

Clearly it is better to allocate the desired space beforehand rather than performing a series of appends.

Let’s see some examples of operations on list.

Examples

First, let us compare two methods for list initialization. The slow option:

foo = []

for _ in range(1_000_000):  # finishes in 82.1 ms
    foo.append(1.0)

A faster option:

foo = [1.0 in range(1_000_000)]  # finishes in 53.3 ms

And a much faster option, but not really a practical one, for it just repeats the one element:

foo = [1.0] * 1_000_000  # finishes in 2.81 ms

Note: beware that this construction works differently for mutable and immutable types.

Now let’s look at the size of one element in a list vs in an array.array and the time needed to scan it.

import random, array, sys
foo_list = [random.random() for _ in range(1_000_000)]

# using 'd' == double 
foo_array = array.array('d', (random.random() for _ in range(1_000_000)))


# need to take size of every element, as they are not stored in the list but referenced
print((sys.getsizeof(foo_list) \
        + sum([sys.getsizeof(i) for i in foo_list]) \
      ) / len(foo_list))
# returns: 32.448728 

print(sys.getsizeof(foo_array) / len(foo_array))
# returns: 8.1838

Note that we do not call sys.getsizeof on every element of the array. It is because they are already counted in the overall size of the array, for they are stored directly in the structure.

Indeed, if we reduce the precision of the decimal number (from 64b to 32b, 'd' to 'f') we get half the size:

foo_array_f = array.array('f', (random.random() for _ in range(1_000_000)))
print(sys.getsizeof(foo_array_f) / len(foo_array_f))
# returns: 4.000064

As we can see, items are much more efficiently stored in array than they are in a list.

Now, let’s compare the scanning speed of list vs array.array:

sum_list = 0.0
sum_array = 0.0

for i in foo_list:  # finishes in 35 ms
    sum_list += i

for i in foo_array:  # finished in 43.7 ms
    sum_array += i

Why is array slower? Even though the elements of an array are efficiently stored in memory, when reading them, an object is created for each of them (I am simplifying a little bit, as there are some optimizations) making the whole scan slower than a scan of a list, which just has to return a reference to the float objects.

Note that, this can be sped up by using the sum() function instead of the loop (to 5.74 ms for list and 14.3 ms for array.

And just as an interesting side note, in numpy, using the numpy.sum() function, the sum takes 0.5 ms.

Conclusion

We saw that using a list for storing or performing operations on float values is quite inefficient. A list of floats is represented in memory as an array of pointers to the PyFloat structure. So for a list of n floats, the consumed memory is approximately 4\*n\*8 bytes (omitting all additive constants and possible overallocation).

Paying attention to how a list is created can also be beneficial. Note that the described “inefficiencies” of list and float are not the only ones. There is a lot more, some of them stemming from the fact that Python is an interpreted language. Some of them can be solved by third-party libraries.

On the other hand, as Donald Knuth once said (or at least it’s attributed to him): premature optimization is the root of all evil. So unless you repeatedly create large lists, you probably should not make the above “list creation” optimizations. However working with real numbers is quite common in Python, in the context of data analysis or machine learning. In such case, it makes sense to use more efficient implementations, such as the one offered by numpy.

Sources